Explanatory Item Response Modeling for Dichotomous and Polytomous Items • eirm

The eirm package, which is essentially a wrapper around the lme4 and blme packages, provides a simple and easy-to-use set of tools for preparing data, estimating explanatory item response theory (IRT) models, extracting model output, and visualizing model results. The primary goal of eirm is to streamline the processes of data preparation, model estimation, and model interpretation for various explanatory IRT models. The functions in the eirm package enable researchers to leverage the power of lme4 and blme for the estimation of explanatory IRT models while providing additional helper functions and visualization tools to better interpret the model output.

Installing `eirm`

The latest version on CRAN can be installed by:

install.packages("eirm")

The development version can be installed by:

devtools::install_github(repo = "okanbulut/eirm")

Note: If you download the Github version and see the following output on your console (or something similar), please choose 3: None from this list. You can simply type 3 in your R console and hit “enter”.

Downloading GitHub repo okanbulut/eirm@master
These packages have more recent versions available.
Which would you like to update?

1: All                                      
2: CRAN packages only                       
3: None                                     
4: Rcpp      (1.0.1     -> 1.0.3    ) [CRAN]
5: RcppEigen (0.3.3.5.0 -> 0.3.3.7.0) [CRAN]
6: plyr      (1.8.4     -> 1.8.5    ) [CRAN]
7: stringi   (1.4.3     -> 1.4.5    ) [CRAN]

Enter one or more numbers, or an empty line to skip updates:

If this also fails, you can run the following lines all together and select 3: None by typing 3 in your R console:

Sys.setenv(R_REMOTES_NO_ERRORS_FROM_WARNINGS=TRUE)
devtools::install_github(repo = "okanbulut/eirm")

Citing `eirm`

To cite eirm in your work, please use the following APA-style citation:

Bulut, O. (2021). eirm: Explanatory item response modeling for dichotomous and polytomous item responses, R package version 0.4. doi: 10.5281/zenodo.4556285 Available from https://CRAN.R-project.org/package=eirm.

Bulut, O., Gorgun, G., & Yildirim-Erbasli, S. N. (2021). Estimating explanatory extensions of dichotomous and polytomous Rasch models: The eirm package in R. Psych, 3(3), 308-321. doi:10.3390/psych3030023

You can also print(citation("eirm"), bibtex = TRUE) to view the citations in BibTeX format.

Shiny GUI for `eirm`

You can use eirmShiny() to open the Shiny GUI for the eirm function:

I plan to expand the Shiny GUI with additional features in the future. Please let me know if you have any suggestions or comments.

Examples

Please visit https://okanbulut.github.io/eirm for documentation and vignettes. For questions about the functionality, you may either contact me via email or also file an issue.

On the package website, you can access two vignettes demonstrating how to use eirm for:

Estimating dichotomous explanatory IRT models with binary data (e.g., 0 = Wrong, 1 = Right)
Estimating polytomous explanatory IRT models with ordinal data (e.g., 1 = No, 2 = Maybe, 3 = Yes)

To demonstrate how the eirm() function works with a quick example, we will estimate the Rasch model (i.e., a fully descriptive model). The following example shows how to estimate item parameters for the verbal aggression data set (see ?VerbAgg for further details). A preview of the VerbAgg data set is shown below:

data("VerbAgg")
head(VerbAgg)
#>   Anger Gender        item    resp id btype  situ mode r2
#> 1    20      M S1WantCurse      no  1 curse other want  N
#> 2    11      M S1WantCurse      no  2 curse other want  N
#> 3    17      F S1WantCurse perhaps  3 curse other want  Y
#> 4    21      F S1WantCurse perhaps  4 curse other want  Y
#> 5    17      F S1WantCurse perhaps  5 curse other want  Y
#> 6    21      F S1WantCurse     yes  6 curse other want  Y

To estimate the Rasch model, a regression-like formula must be defined: formula = "r2 ~ -1 + item + (1|id)". In the formula,

r2 is the variable for dichotomous item responses
-1 removes the intercept from the model and yields parameter estimates for all items in the data set. With 1 (instead of -1), an intercept representing the parameter of the first item and relative parameters for the remaining items (i.e., distance from the parameter of the first item) would be estimated.
itemis the variable representing item IDs in the data set
(1|id) refers to the random effects for persons represented by the id column in the data set.

The output for the Rasch model is shown below:

mod1 <- eirm(formula = "r2 ~ -1 + item + (1|id)", data = VerbAgg)
print(mod1)


EIRM formula: "r2 ~ -1 + item + (1|id)" 

Number of persons: 316 

Number of observations: 7584 

Number of predictors: 24 

Parameter Estimates:

                Easiness   S.E.  z-value   p-value
itemS1WantCurse  1.22107 0.1611   7.5794 3.470e-14
itemS1WantScold  0.56477 0.1525   3.7032 2.129e-04
itemS1WantShout  0.08009 0.1505   0.5323 5.945e-01
itemS2WantCurse  1.74879 0.1738  10.0632 8.035e-24
itemS2WantScold  0.70772 0.1538   4.6020 4.184e-06
itemS2WantShout  0.01172 0.1504   0.0779 9.379e-01
itemS3WantCurse  0.52947 0.1522   3.4777 5.057e-04
itemS3WantScold -0.68637 0.1542  -4.4506 8.564e-06
itemS3WantShout -1.52694 0.1692  -9.0222 1.843e-19
itemS4wantCurse  1.08204 0.1587   6.8193 9.151e-12
itemS4WantScold -0.34938 0.1515  -2.3062 2.110e-02
itemS4WantShout -1.04402 0.1591  -6.5628 5.280e-11
itemS1DoCurse    1.22107 0.1611   7.5794 3.470e-14
itemS1DoScold    0.38962 0.1514   2.5739 1.006e-02
itemS1DoShout   -0.87122 0.1565  -5.5680 2.576e-08
itemS2DoCurse    0.87264 0.1557   5.6063 2.067e-08
itemS2DoScold   -0.05668 0.1505  -0.3766 7.065e-01
itemS2DoShout   -1.48186 0.1681  -8.8152 1.195e-18
itemS3DoCurse   -0.21104 0.1509  -1.3988 1.619e-01
itemS3DoScold   -1.50431 0.1687  -8.9189 4.709e-19
itemS3DoShout   -2.97500 0.2334 -12.7483 3.186e-37
itemS4DoCurse    0.70772 0.1538   4.6020 4.184e-06
itemS4DoScold   -0.38422 0.1517  -2.5328 1.132e-02
itemS4DoShout   -1.99947 0.1839 -10.8750 1.516e-27

Note: The estimated parameters above represent 'easiness'.
Use difficulty = TRUE to get difficulty parameters.

By default, the eirm function returns the easiness parameters because the function uses a regression model parameterization where positive parameters indicate positive association with the dependent variable. In order to print the difficulty parameters (instead of easiness), print(mod1, difficulty = TRUE) must be used:

print(mod1, difficulty = TRUE)

Parameter Estimates:

                Difficulty   S.E.  z-value   p-value
itemS1WantCurse   -1.22107 0.1611   7.5794 3.470e-14
itemS1WantScold   -0.56477 0.1525   3.7032 2.129e-04
itemS1WantShout   -0.08009 0.1505   0.5323 5.945e-01
itemS2WantCurse   -1.74879 0.1738  10.0632 8.035e-24
itemS2WantScold   -0.70772 0.1538   4.6020 4.184e-06
itemS2WantShout   -0.01172 0.1504   0.0779 9.379e-01
itemS3WantCurse   -0.52947 0.1522   3.4777 5.057e-04
itemS3WantScold    0.68637 0.1542  -4.4506 8.564e-06
itemS3WantShout    1.52694 0.1692  -9.0222 1.843e-19
itemS4wantCurse   -1.08204 0.1587   6.8193 9.151e-12
itemS4WantScold    0.34938 0.1515  -2.3062 2.110e-02
itemS4WantShout    1.04402 0.1591  -6.5628 5.280e-11
itemS1DoCurse     -1.22107 0.1611   7.5794 3.470e-14
itemS1DoScold     -0.38962 0.1514   2.5739 1.006e-02
itemS1DoShout      0.87122 0.1565  -5.5680 2.576e-08
itemS2DoCurse     -0.87264 0.1557   5.6063 2.067e-08
itemS2DoScold      0.05668 0.1505  -0.3766 7.065e-01
itemS2DoShout      1.48186 0.1681  -8.8152 1.195e-18
itemS3DoCurse      0.21104 0.1509  -1.3988 1.619e-01
itemS3DoScold      1.50431 0.1687  -8.9189 4.709e-19
itemS3DoShout      2.97500 0.2334 -12.7483 3.186e-37
itemS4DoCurse     -0.70772 0.1538   4.6020 4.184e-06
itemS4DoScold      0.38422 0.1517  -2.5328 1.132e-02
itemS4DoShout      1.99947 0.1839 -10.8750 1.516e-27

Note: The estimated parameters above represent 'difficulty'.

The mod1 object is essentially a glmerMod-class object from the lme4 package (Bates, Maechler, Bolker, & Walker (2015)). All glmerMod results for the estimated model can seen with mod1$model. For example, estimated random effects for persons (i.e., theta estimates) can be obtained using:

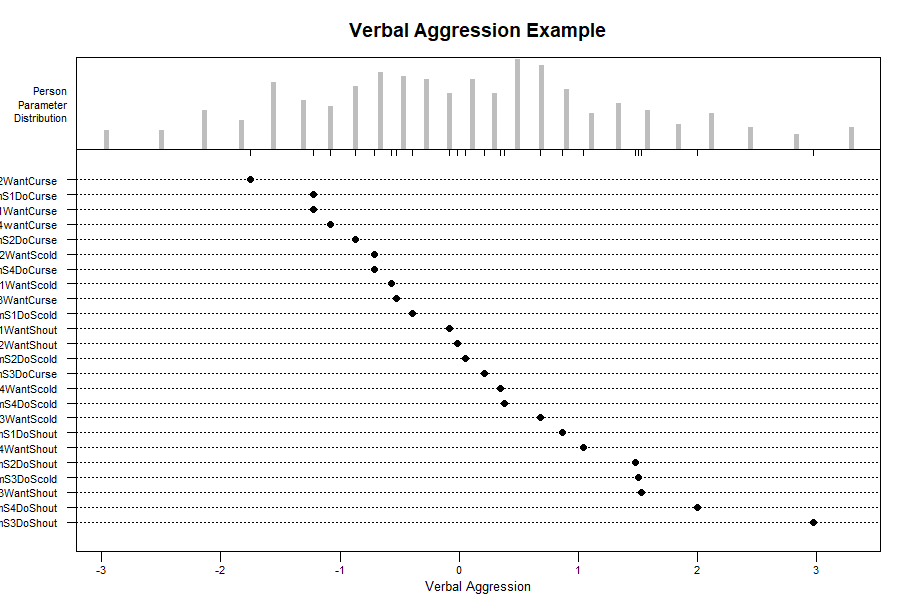
theta <- ranef(mod1$model)$id

To visualize the results, we can create an item-person map using plot(mod1), which returns the following plot. Note that this plot is a modified version of the plotPImap function from the eRm package (Mair, Hatzinger, Maier, Rusch, & Debelak, 2020).

plot(mod1)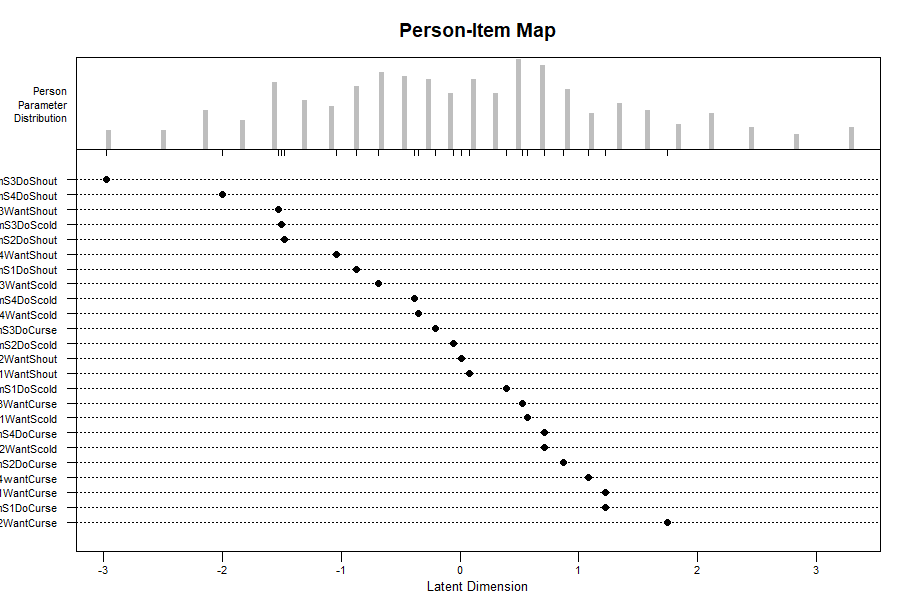

Aesthetic elements such as axis labels and plot title can be added to the plot. For example, the following code updates the x-axis label and the main plot title (see ?plot.eirm for further details).

plot(mod1, difficulty = TRUE, main = "Verbal Aggression Example", 
     latdim = "Verbal Aggression")

which will show the difficulty parameters (instead of easiness), change the main title above the plot, and change the x-axis – the name for the latent trait being measured.

eirm: Explanatory Item Response Modeling

Installing eirm

Citing eirm

Shiny GUI for eirm

Examples

Installing `eirm`

Citing `eirm`

Shiny GUI for `eirm`